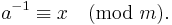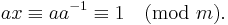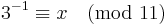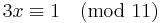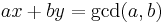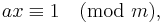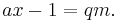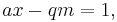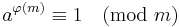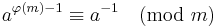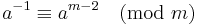Modular multiplicative inverse

The modular multiplicative inverse of an integer a modulo m is an integer x such that

$a^{-1} \equiv x \pmod{m}.$

That is, it is the multiplicative inverse in the ring of integers modulo m. This is equivalent to

$ax \equiv aa^{-1} \equiv 1 \pmod{m}.$

The multiplicative inverse of a modulo m exists if and only if a and m are coprime (i.e., if gcd(a, m) = 1). If the modular multiplicative inverse of a modulo m exists, the operation of division by a modulo m can be defined as multiplying by the inverse, which is in essence the same concept as division in the field of reals.

1 Explanation
2 Computation
- 2.1 Extended Euclidean algorithm
- 2.2 Using Euler's theorem
3 See also
4 References

Explanation

When the inverse exists, it is always unique in 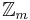$\mathbb{Z}_m$ where m is the modulus. Therefore, the x that is selected as the modular multiplicative inverse is generally a member of 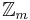$\mathbb{Z}_m$ for most applications.

For example,

$3^{-1} \equiv x \pmod{11}$

yields

$3x \equiv 1 \pmod{11}$

The smallest x that solves this congruence is 4; therefore, the modular multiplicative inverse of 3 (mod 11) is 4. However, another x that solves the congruence is 15 (easily found by adding m, which is 11, to the found inverse).

Computation

Extended Euclidean algorithm

The modular multiplicative inverse of a modulo m can be found with the extended Euclidean algorithm. The algorithm finds solutions to Bézout's identity

$ax %2B by = \gcd(a, b)\,$

where a, b are given and x, y, and gcd(a, b) are the integers that the algorithm discovers. So, since the modular multiplicative inverse is the solution to

$ax \equiv 1 \pmod{m},$

by the definition of congruence, m | ax − 1, which means that m is a divisor of ax − 1. This, in turn, means that

$ax - 1 = qm.\,$

Rearranging produces

$ax - qm = 1,\,$

with a and m given, x the inverse, and q an integer multiple that will be discarded. This is the exact form of equation that the extended Euclidean algorithm solves—the only difference being that gcd(a, m) = 1 is predetermined instead of discovered. Thus, a needs to be coprime to the modulus, or the inverse won't exist. The inverse is x, and q is discarded.

This algorithm runs in time O(log(m)²), assuming |a| < m, and is generally more efficient than exponentiation.

Using Euler's theorem

As an alternative to the extended Euclidean algorithm, Euler's theorem may be used to compute modular inverse:^[1]

According to Euler's theorem, if a is coprime to m, that is, gcd(a, m) = 1, then

$a^{\varphi(m)} \equiv 1 \pmod{m}$

where φ(m) is Euler's totient function. This follows from the fact that a belongs to the multiplicative group (Z/mZ)^* iff a is coprime to m. Therefore the modular multiplicative inverse can be found directly:

$a^{\varphi(m)-1} \equiv a^{-1} \pmod{m}$

In the special case when m is a prime, the modular inverse is given by the above equation as:

$\! a^{-1} \equiv a^{m-2} \pmod{m}$

This method is generally slower than the extended Euclidean algorithm, but is sometimes used when an implementation for modular exponentiation is already available. Some disadvantages of this method include:

the required knowledge of φ(m), whose most efficient computation requires m's factorization. Factorization is widely believed to be a mathematically hard problem. However, calculating φ(m) is trivial in some common cases such as when m is known to be prime or a power of a prime.
exponentiation. Though it can be implemented more efficiently using modular exponentiation, when large values of m are involved this is most efficiently computed with the Montgomery reduction method. This algorithm itself requires a modular inverse mod m, which is what we wanted to calculate in the first place. Without the Montgomery method, we're left with standard binary exponentiation which requires division mod m at every step, a slow operation when m is large. Furthermore, any kind of modular exponentiation is a taxing operation with computational complexity O(log φ(m)) = O(log m).

References

^ Thomas Koshy. Elementary number theory with applications, 2nd edition. ISBN 978-0-12-372487-8. P. 346.